Note
Go to the end to download the full example code
Linking KeOps with GPytorch
Out-of-the-box, KeOps only provides limited support for
Kriging
or Gaussian process regression:
the KernelSolve operator
implements a conjugate gradient solver for kernel linear systems…
and that’s about it.
Fortunately though, KeOps can easily be used
as a scalable GPU backend for versatile, high-level libraries such
as GPytorch: in this notebook,
we show how to plug KeOps’ pykeops.torch.LazyTensor
within the first regression tutorial
of GPytorch’s documentation.
Due to hard-coded constraints within the structure of GPytorch, the syntax presented below is pretty verbose… But we’re working on it! Needless to say, feel free to let us know if you encounter any unexpected behavior with this experimental KeOps-GPytorch interface.
Note
The GPytorch team has now integrated explicit KeOps kernels within their repository: they are documented in this tutorial and make the handcrafted example below somewhat obsolete. Nevertheless, we keep this page online for the sake of completeness: it may be useful to advanced users who wish to use custom KeOps kernels with GPytorch.
Setup
Standard imports, including gpytorch:
import gpytorch
import math
import torch
from matplotlib import pyplot as plt
use_cuda = torch.cuda.is_available()
dtype = torch.cuda.FloatTensor if use_cuda else torch.FloatTensor
We generate a toy dataset: some regularly spaced samples on the unit interval, and a sinusoid signal corrupted by a small Gaussian noise.
N = 1000 if use_cuda else 100
train_x = torch.linspace(0, 1, N).type(dtype)
train_y = torch.sin(train_x * (2 * math.pi)) + 0.2 * torch.randn(train_x.size()).type(
dtype
)
Defining a new KeOps RBF kernel
Internally, GPytorch relies on LazyTensors
parameterized by explicit torch Tensors - and nothing else.
To let GPytorch use our KeOps CUDA routines, we should thus create
a new class of gpytorch.lazy.LazyTensor, encoding an implicit
kernel matrix built from raw point clouds x_i and y_j.
Note
Ideally, we’d like to be able to export KeOps LazyTensors directly as GPytorch objects, but the reliance of the latter’s internal engine on explicit torch.Tensor variables is a hurdle that we could not bypass easily. Working on this problem with the GPytorch team, we hope to provide a simpler interface in future releases.
from pykeops.torch import LazyTensor
class KeOpsRBFLazyTensor(gpytorch.lazy.LazyTensor):
def __init__(self, x_i, y_j):
"""Creates a symbolic Gaussian RBF kernel out of two point clouds `x_i` and `y_j`."""
super().__init__(
x_i, y_j
) # GPytorch will remember that self was built from x_i and y_j
self.x_i, self.y_j = x_i, y_j # Useful to define a symbolic transpose
with torch.autograd.enable_grad(): # N.B.: gpytorch operates in no_grad mode
x_i, y_j = (
LazyTensor(self.x_i[:, None, :]),
LazyTensor(self.y_j[None, :, :]),
)
K_xy = (
-((x_i - y_j) ** 2).sum(-1) / 2
).exp() # Compute the kernel matrix symbolically...
self.K = K_xy # ... and store it for later use
def _matmul(self, M):
"""Kernel-Matrix multiplication."""
return self.K @ M
def _size(self):
"""Shape attribute."""
return torch.Size(self.K.shape)
def _transpose_nonbatch(self):
"""Symbolic transpose operation."""
return KeOpsRBFLazyTensor(self.y_j, self.x_i)
def _get_indices(self, row_index, col_index, *batch_indices):
"""Returns a (small) explicit sub-matrix, used e.g. for Nystroem approximation."""
X_i = self.x_i[row_index]
Y_j = self.y_j[col_index]
return (-((X_i - Y_j) ** 2).sum(-1) / 2).exp() # Genuine torch.Tensor
def _quad_form_derivative(self, *args, **kwargs):
"""As of gpytorch v0.3.2, the default implementation returns a list instead of a tuple..."""
return tuple(super()._quad_form_derivative(*args, **kwargs)) # Bugfix!
We can now create a new GPytorch Kernel object, wrapped around our KeOps+GPytorch LazyTensor:
class KeOpsRBFKernel(gpytorch.kernels.Kernel):
"""Simple KeOps re-implementation of 'gpytorch.kernels.RBFKernel'."""
has_lengthscale = True
def forward(self, x1, x2, diag=False, **params):
if diag: # A Gaussian RBF kernel only has "ones" on the diagonal
return torch.ones(len(x1)).type_as(x1)
else:
if x1.dim() == 1:
x1 = x1.view(-1, 1)
if x2.dim() == 1:
x2 = x2.view(-1, 1)
# Rescale the input data...
x_i, y_j = x1.div(self.lengthscale), x2.div(self.lengthscale)
return KeOpsRBFLazyTensor(
x_i, y_j
) # ... and return it as a gyptorch.lazy.LazyTensor
And use it to define a new Gaussian Process model:
# We will use the simplest form of GP model, exact inference
class KeOpsGPModel(gpytorch.models.ExactGP):
def __init__(self, train_x, train_y, likelihood):
super().__init__(train_x, train_y, likelihood)
self.mean_module = gpytorch.means.ConstantMean()
self.covar_module = gpytorch.kernels.ScaleKernel(KeOpsRBFKernel())
def forward(self, x):
mean_x = self.mean_module(x)
covar_x = self.covar_module(x)
return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)
N.B., for the sake of comparison: the GPytorch documentation went with
the code below, using the standard gpytorch.kernels.RBFKernel()
instead of our custom KeOpsRBFKernel():
class ExactGPModel(gpytorch.models.ExactGP):
def __init__(self, train_x, train_y, likelihood):
super(ExactGPModel, self).__init__(train_x, train_y, likelihood)
self.mean_module = gpytorch.means.ConstantMean()
self.covar_module = gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel())
def forward(self, x):
mean_x = self.mean_module(x)
covar_x = self.covar_module(x)
return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)
That’s it! We can now initialize our likelihood and model, as recommended by the documentation:
if use_cuda:
likelihood = gpytorch.likelihoods.GaussianLikelihood().cuda()
model = KeOpsGPModel(train_x, train_y, likelihood).cuda()
else:
likelihood = gpytorch.likelihoods.GaussianLikelihood()
model = KeOpsGPModel(train_x, train_y, likelihood)
GP training
The code below is now a direct copy-paste from the GPytorch 101 tutorial:
# Find optimal model hyperparameters
model.train()
likelihood.train()
# Use the adam optimizer
optimizer = torch.optim.Adam(
[
{"params": model.parameters()},
],
lr=0.1, # Includes GaussianLikelihood parameters
)
# "Loss" for GPs - the marginal log likelihood
mll = gpytorch.mlls.ExactMarginalLogLikelihood(likelihood, model)
training_iter = 50
for i in range(training_iter):
# Zero gradients from previous iteration
optimizer.zero_grad()
# Output from model
output = model(train_x)
# Calc loss and backprop gradients
loss = -mll(output, train_y)
loss.backward()
if i % 10 == 0 or i == training_iter - 1:
print(
"Iter %d/%d - Loss: %.3f lengthscale: %.3f noise: %.3f"
% (
i + 1,
training_iter,
loss.item(),
model.covar_module.base_kernel.lengthscale.item(),
model.likelihood.noise.item(),
)
)
optimizer.step()
Iter 1/50 - Loss: 0.863 lengthscale: 0.693 noise: 0.693
Iter 11/50 - Loss: 0.418 lengthscale: 0.335 noise: 0.311
Iter 21/50 - Loss: 0.067 lengthscale: 0.235 noise: 0.125
Iter 31/50 - Loss: -0.124 lengthscale: 0.223 noise: 0.052
Iter 41/50 - Loss: -0.114 lengthscale: 0.241 noise: 0.033
Iter 50/50 - Loss: -0.118 lengthscale: 0.265 noise: 0.036
Prediction and display
Get into evaluation (predictive posterior) mode
model.eval()
likelihood.eval()
GaussianLikelihood(
(noise_covar): HomoskedasticNoise(
(raw_noise_constraint): GreaterThan(1.000E-04)
)
)
Test points are regularly spaced along [0,1].
We make predictions by feeding our model through the likelihood:
with torch.no_grad(), gpytorch.settings.fast_pred_var():
test_x = torch.linspace(0, 1, 51).type(dtype)
observed_pred = likelihood(model(test_x))
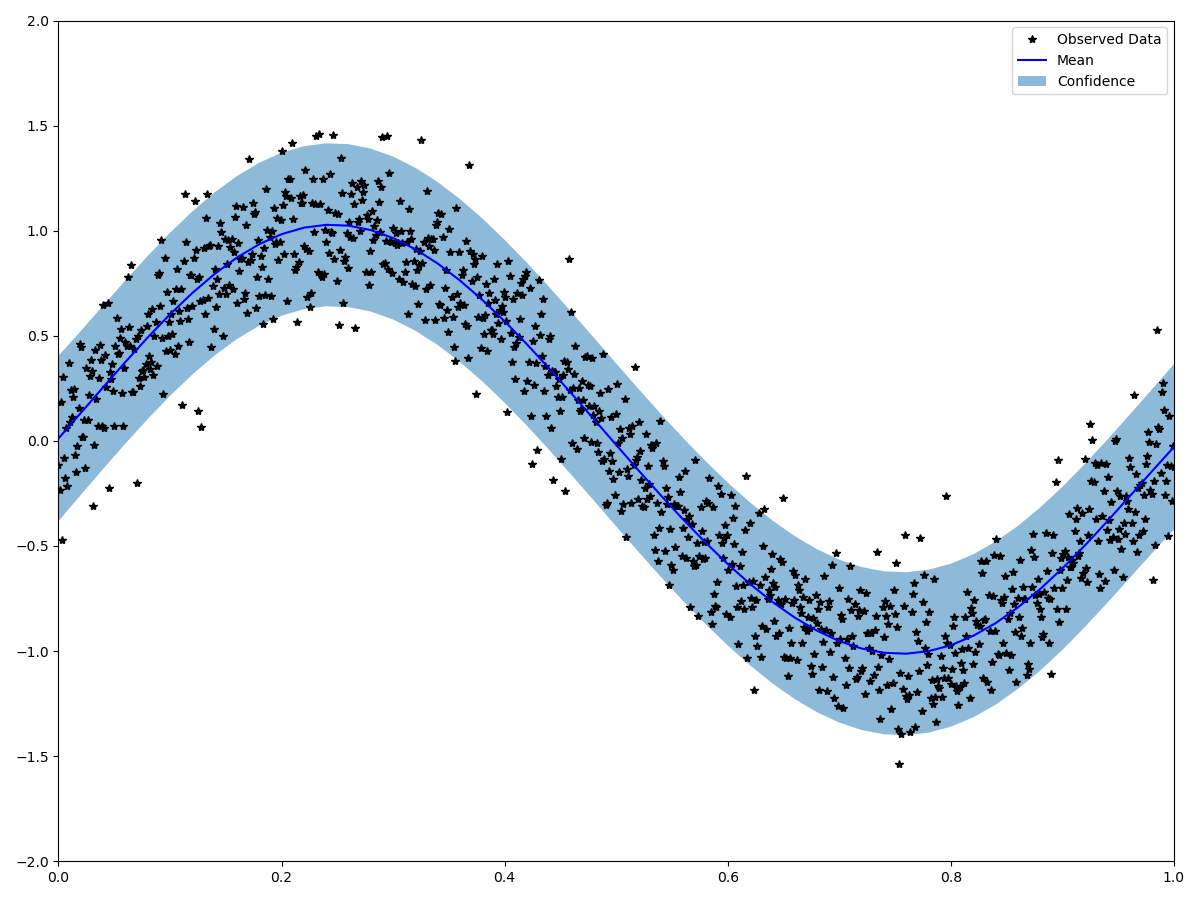
Display:
with torch.no_grad():
# Initialize plot
f, ax = plt.subplots(1, 1, figsize=(12, 9))
# Get upper and lower confidence bounds
lower, upper = observed_pred.confidence_region()
# Plot training data as black stars
ax.plot(train_x.cpu().numpy(), train_y.cpu().numpy(), "k*")
# Plot predictive means as blue line
ax.plot(test_x.cpu().numpy(), observed_pred.mean.cpu().numpy(), "b")
# Shade between the lower and upper confidence bounds
ax.fill_between(
test_x.cpu().numpy(), lower.cpu().numpy(), upper.cpu().numpy(), alpha=0.5
)
ax.set_ylim([-3, 3])
ax.legend(["Observed Data", "Mean", "Confidence"])
plt.axis([0, 1, -2, 2])
plt.tight_layout()
plt.show()
Total running time of the script: (0 minutes 2.214 seconds)