Gallery of examples
These self-contained examples showcase the features of the geomloss module.
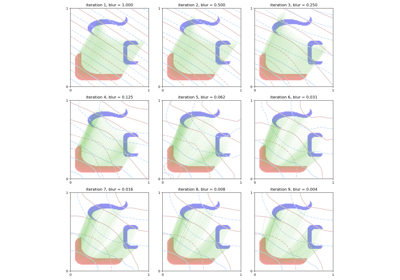
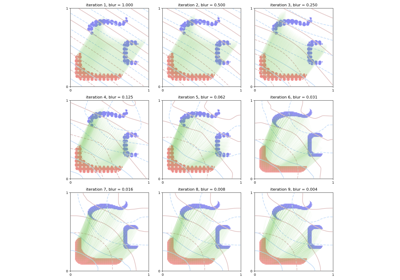
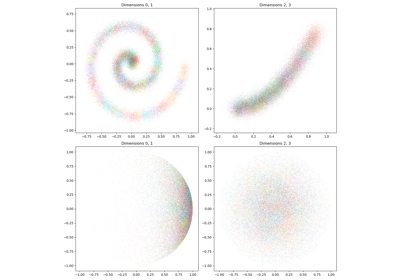
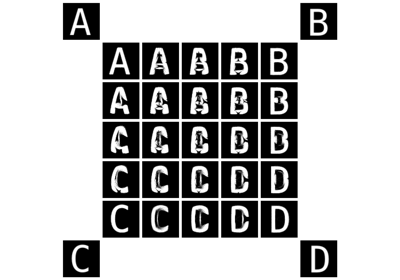
Kernel vs. Hausdorff vs. Sinkhorn
See the difference between our kernel, hausdorff and sinkhorn loss functions:
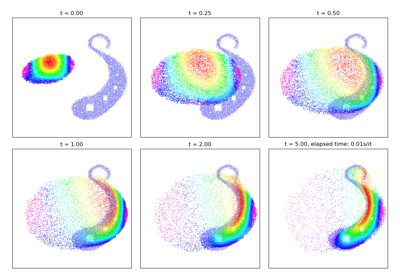
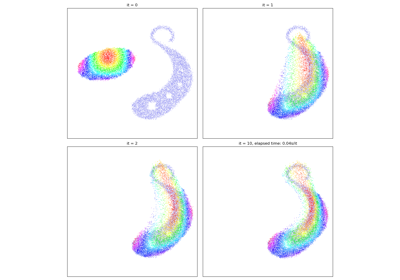
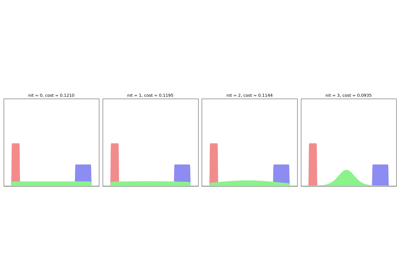
The multiscale Sinkhorn algorithm
Outperform the baseline Auction and Sinkhorn algorithms by a factor x50-100 with adaptive coarse-to-fine strategies:
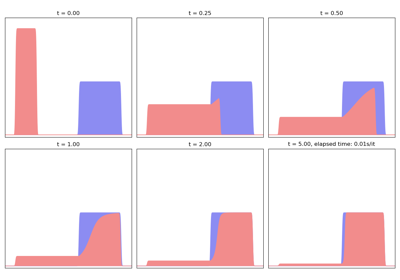
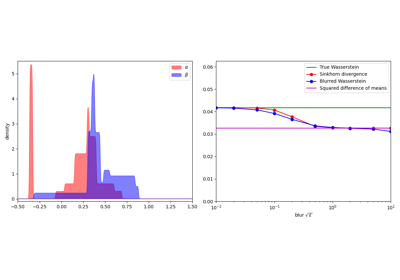
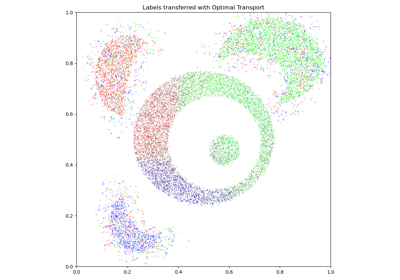
Optimal Transport
Use the sinkhorn loss as an affordable, drop-in replacement for the Wasserstein distance:

Creating a fancy interpolation video between 3D meshes.
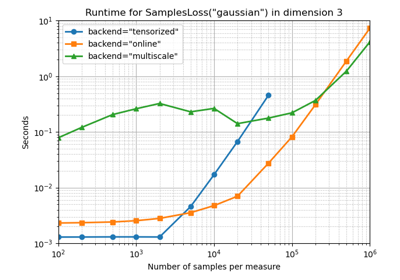
Performances
Select the hyper-parameters that are best suited to your data:
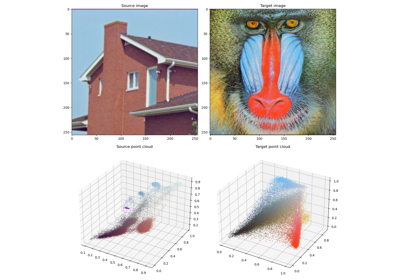
Scaling up to brain tractograms – with Pierre Roussillon
Use unbalanced, regularized Optimal Transport to process white matter fiber tracks. The scripts presented below should allow you to reproduce the experiments of the Miccai 2019 paper Fast and scalable Optimal Transport for brain tractograms by Jean Feydy*, Pierre Roussillon*, Alain Trouvé and Pietro Gori.