Basic functions which support complex arithmetic in R, in addition to
the arithmetic operators +, -, *, /, and ^.
Details
Complex vectors can be created with complex. The vector can be
specified either by giving its length, its real and imaginary parts, or
modulus and argument. (Giving just the length generates a vector of
complex zeroes.)
as.complex attempts to coerce its argument to be of complex
type: like as.vector it strips attributes including
names. Up to R versions 3.2.x, all forms of NA and NaN
were coerced to a complex NA, i.e., the NA_complex_
constant, for which both the real and imaginary parts are NA.
Since R 3.3.0, typically only objects which are NA in parts
are coerced to complex NA, but others with NaN parts,
are not. As a consequence, complex arithmetic where only
NaN's (but no NA's) are involved typically will
not give complex NA but complex numbers with real or
imaginary parts of NaN.
Note that is.complex and is.numeric are never both
TRUE.
The functions Re, Im, Mod, Arg and
Conj have their usual interpretation as returning the real
part, imaginary part, modulus, argument and complex conjugate for
complex values. The modulus and argument are also called the polar
coordinates. If \(z = x + i y\) with real \(x\) and \(y\), for
\(r = Mod(z) = \sqrt{x^2 + y^2}\),
and \(\phi = Arg(z)\), \(x = r \cos(\phi)\) and
\(y = r \sin(\phi)\). They are all
internal generic primitive functions: methods can be
defined for them
individually or via the Complex
group generic.
In addition to the arithmetic operators (see Arithmetic)
+, -, *, /, and ^, the elementary
trigonometric, logarithmic, exponential, square root and hyperbolic
functions are implemented for complex values.
Matrix multiplications (%*%, crossprod,
tcrossprod) are also defined for complex matrices
(matrix), and so are solve,
eigen or svd.
Internally, complex numbers are stored as a pair of double
precision numbers, either or both of which can be NaN
(including NA, see NA_complex_ and above) or
plus or minus infinity.
Examples
require(graphics)
0i ^ (-3:3)
#> [1] Inf+0i Inf+0i Inf+0i 1+0i 0+0i 0+0i 0+0i
matrix(1i^ (-6:5), nrow = 4) #- all columns are the same
#> [,1] [,2] [,3]
#> [1,] -1+0i -1+0i -1+0i
#> [2,] 0-1i 0-1i 0-1i
#> [3,] 1+0i 1+0i 1+0i
#> [4,] 0+1i 0+1i 0+1i
0 ^ 1i # a complex NaN
#> [1] NaN+NaNi
## create a complex normal vector
z <- complex(real = stats::rnorm(100), imaginary = stats::rnorm(100))
## or also (less efficiently):
z2 <- 1:2 + 1i*(8:9)
## The Arg(.) is an angle:
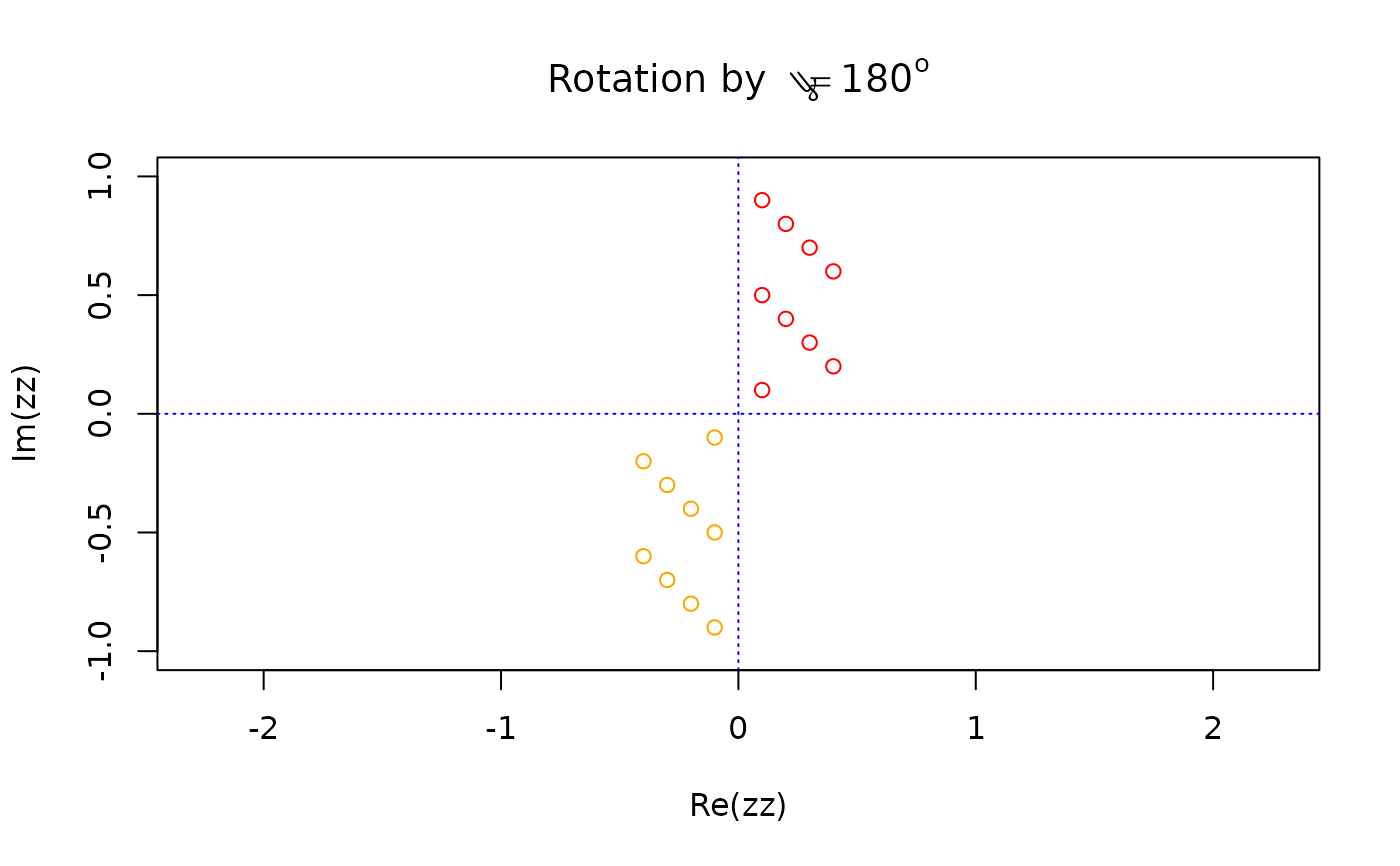
zz <- (rep(1:4, length.out = 9) + 1i*(9:1))/10
zz.shift <- complex(modulus = Mod(zz), argument = Arg(zz) + pi)
plot(zz, xlim = c(-1,1), ylim = c(-1,1), col = "red", asp = 1,
main = expression(paste("Rotation by "," ", pi == 180^o)))
abline(h = 0, v = 0, col = "blue", lty = 3)
points(zz.shift, col = "orange")
showC <- function(z) noquote(sprintf("(R = %g, I = %g)", Re(z), Im(z)))
## The exact result of this *depends* on the platform, compiler, math-library:
(NpNA <- NaN + NA_complex_) ; str(NpNA) # *behaves* as 'cplx NA' ..
#> [1] NA
#> cplx NA
stopifnot(is.na(NpNA), is.na(NA_complex_), is.na(Re(NA_complex_)), is.na(Im(NA_complex_)))
showC(NpNA)# but not always is {shows '(R = NaN, I = NA)' on some platforms}
#> [1] (R = NA, I = NA)
## and this is not TRUE everywhere:
identical(NpNA, NA_complex_)
#> [1] TRUE
showC(NA_complex_) # always == (R = NA, I = NA)
#> [1] (R = NA, I = NA)