Sum reduction

Let’s compute the (3000,3) tensor \(c\) whose entries \(c_i^u\) are given by:

\[c_i^u = \sum_j (p-a_j)^2 \exp(x_i^u+y_j^u)\]

where

• \(x\) is a (3000,3) tensor, with entries \(x_i^u\).

• \(y\) is a (5000,3) tensor, with entries \(y_j^u\).

• \(a\) is a (5000,1) tensor, with entries \(a_j\).

• \(p\) is a scalar, encoded as a vector of size (1,).

Setup

Standard imports:

import time

import matplotlib.pyplot as plt
import torch
from torch.autograd import grad

from pykeops.torch import Genred

Declare random inputs:

M = 3000
N = 5000

# Choose the storage place for our data : CPU (host) or GPU (device) memory.
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

dtype = "float32"  # Could be 'float32' or 'float64'
torchtype = torch.float32 if dtype == "float32" else torch.float64

x = torch.randn(M, 3, dtype=torchtype, device=device)
y = torch.randn(N, 3, dtype=torchtype, device=device, requires_grad=True)
a = torch.randn(N, 1, dtype=torchtype, device=device)
p = torch.randn(1, dtype=torchtype, device=device)

Define a custom formula

formula = "Square(p-a)*Exp(x+y)"
variables = [
    "x = Vi(3)",  # First arg   : i-variable, of size 3
    "y = Vj(3)",  # Second arg  : j-variable, of size 3
    "a = Vj(1)",  # Third arg   : j-variable, of size 1 (scalar)
    "p = Pm(1)",
]  # Fourth  arg : Parameter,  of size 1 (scalar)

Our sum reduction is performed over the index \(j\), i.e. on the axis 1 of the kernel matrix. The output c is an \(x\)-variable indexed by \(i\).

my_routine = Genred(formula, variables, reduction_op="Sum", axis=1)
c = my_routine(x, y, a, p)

Compute the gradient

Now, let’s compute the gradient of \(c\) with respect to \(y\). Since \(c\) is not scalar valued, its “gradient” \(\partial c\) should be understood as the adjoint of the differential operator, i.e. as the linear operator that:

• takes as input a new tensor \(e\) with the shape of \(c\)

• outputs a tensor \(g\) with the shape of \(y\)

such that for all variation \(\delta y\) of \(y\) we have:

\[\langle \text{d} c . \delta y , e \rangle = \langle g , \delta y \rangle = \langle \delta y , \partial c . e \rangle\]

Backpropagation is all about computing the tensor \(g=\partial c . e\) efficiently, for arbitrary values of \(e\):

# Declare a new tensor of shape (M,3) used as the input of the gradient operator.
# It can be understood as a "gradient with respect to the output c"
# and is thus called "grad_output" in the documentation of PyTorch.
e = torch.rand_like(c)

# Call the gradient op:
start = time.time()

# PyTorch remark : grad(c, y, e) alone outputs a length 1 tuple, hence the need for [0].
g = grad(c, y, e)[0]  # g = [∂_y c].e

print(
    "Time to compute gradient of convolution operation with KeOps: ",
    round(time.time() - start, 5),
    "s",
)

Time to compute gradient of convolution operation with KeOps:  0.01876 s

The equivalent code with a “vanilla” pytorch implementation

g_torch = (
    (
        (p - a.transpose(0, 1))[:, None] ** 2
        * torch.exp(x.transpose(0, 1)[:, :, None] + y.transpose(0, 1)[:, None, :])
        * e.transpose(0, 1)[:, :, None]
    )
    .sum(dim=1)
    .transpose(0, 1)
)

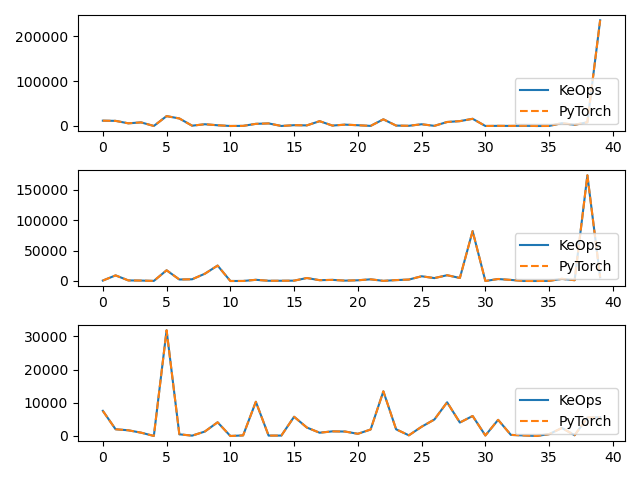
# Plot the results next to each other:
for i in range(3):
    plt.subplot(3, 1, i + 1)
    plt.plot(g.detach().cpu().numpy()[:40, i], "-", label="KeOps")
    plt.plot(g_torch.detach().cpu().numpy()[:40, i], "--", label="PyTorch")
    plt.legend(loc="lower right")
plt.tight_layout()
plt.show()